Справочный материал
Примеры
Обратите внимание!
Видео
Модели
Пройти тесты
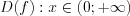 ;
; 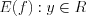 .
. 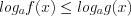 (
( ,
,  ,
,  ), (7.17)
), (7.17)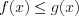 ; (7.17.1)
; (7.17.1)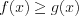 . (7.17.2)
. (7.17.2)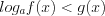 (7.18)
(7.18)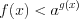 ; (7.18.1)
; (7.18.1)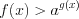 . (7.18.2)
. (7.18.2)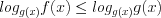 , (7.19)
, (7.19)
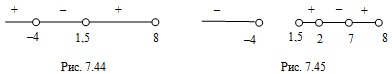
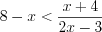 ,
, 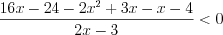 ,
,  ,
, 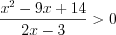 .
. 
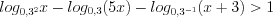 ,
,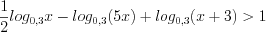 ,
,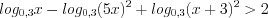 ,
, 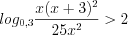 .
. 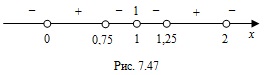
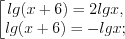
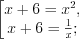

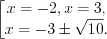
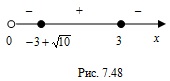

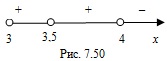


Логарифмическими называют неравенства, содержащие логарифмическую функцию.
Решение логарифмических неравенств основано на свойствах логарифмической функции.
Логарифмической называют функцию вида 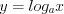 , где
, где  и
и  .
.
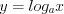 , где
, где  и
и  .
. 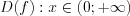 ;
; 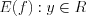 .
. При  функция возрастает, а при
функция возрастает, а при  – убывает.
– убывает.
 функция возрастает, а при
функция возрастает, а при  – убывает.
– убывает.Методы решений неравенств
1. Если неравенство имеет вид
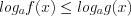 (
( ,
,  ,
,  ), (7.17)
), (7.17)где 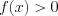 и
и 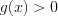 то:
то:
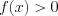 и
и 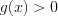 то:
то: а) при условии, что  получим
получим
 получим
получим 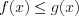 ; (7.17.1)
; (7.17.1)б) при условии, что  получим
получим
 получим
получим 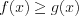 . (7.17.2)
. (7.17.2)2. Если неравенство имеет вид
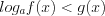 (7.18)
(7.18)и 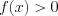 , то:
, то:
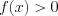 , то:
, то: а) при условии, что  получим
получим
 получим
получим 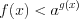 ; (7.18.1)
; (7.18.1)б) при условии, что  получим
получим
 получим
получим 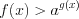 . (7.18.2)
. (7.18.2)3. Если неравенство имеет вид
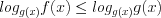 , (7.19)
, (7.19)то решают совокупность систем неравенств:
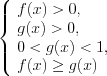 (7.19.1) и
(7.19.1) и  (7.19.2)
(7.19.2)
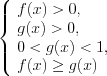 (7.19.1) и
(7.19.1) и  (7.19.2)
(7.19.2)Пример 1. Найдите решение неравенства  .
.
 .
.Решение. ОДЗ: 

Поскольку решением первого неравенства является промежуток 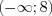 , то второе неравенство системы решим на этом промежутке методом интервалов. Согласно рисунку 7.44 запишем:
, то второе неравенство системы решим на этом промежутке методом интервалов. Согласно рисунку 7.44 запишем: 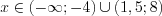 .
.
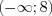 , то второе неравенство системы решим на этом промежутке методом интервалов. Согласно рисунку 7.44 запишем:
, то второе неравенство системы решим на этом промежутке методом интервалов. Согласно рисунку 7.44 запишем: 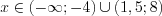 .
.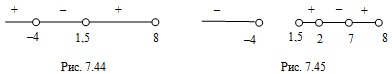
Так как 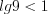 , то :
, то :
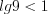 , то :
, то : 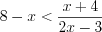 ,
, 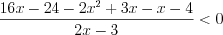 ,
,  ,
, 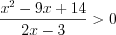 .
. Решим последнее неравенство методом интервалов на ОДЗ исходного неравенства (рис. 7.45) и получим: 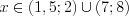 .
.
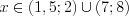 .
. Ответ: 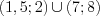 .
.
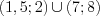 .
.Пример 2. Найдите середину промежутка, на котором выполняется неравенство 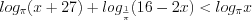 .
.
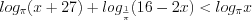 .
.Решение. ОДЗ: 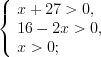
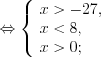
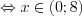 .
.
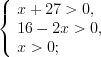
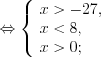
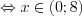 .
.Выполним преобразования: 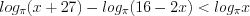
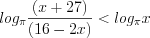 .
.
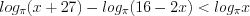
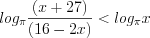 .
. Поскольку основание логарифма 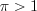 , то данное неравенство равносильно неравенству
, то данное неравенство равносильно неравенству 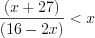 ,
, 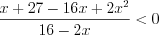 ,
, 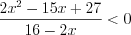 . Решение этого неравенства показано на рисунке 7.46 :
. Решение этого неравенства показано на рисунке 7.46 :  .
.
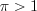 , то данное неравенство равносильно неравенству
, то данное неравенство равносильно неравенству 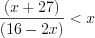 ,
, 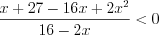 ,
, 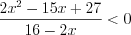 . Решение этого неравенства показано на рисунке 7.46 :
. Решение этого неравенства показано на рисунке 7.46 :  .
.
Найдем середину интервала: 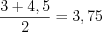 .
.
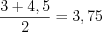 .
.Ответ: 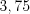 .
.
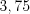 .
.Пример 3. Решите неравенство 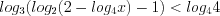 .
.
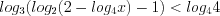 .
.Решение. ОДЗ: 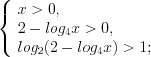
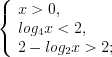
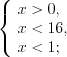
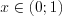 .
.
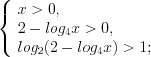
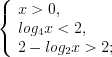
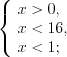
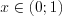 .
.Учитывая, что  , получим:
, получим: 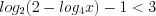 ,
, 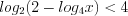 ,
, 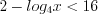 ,
,  ,
, 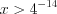 ,
, 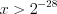 . Учитывая ОДЗ неравенства, запишем его решение:
. Учитывая ОДЗ неравенства, запишем его решение: 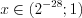 .
.
 , получим:
, получим: 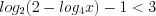 ,
, 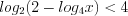 ,
, 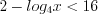 ,
,  ,
, 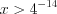 ,
, 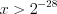 . Учитывая ОДЗ неравенства, запишем его решение:
. Учитывая ОДЗ неравенства, запишем его решение: 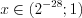 .
.Ответ: 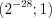 .
.
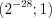 .
.Пример 4. Решите неравенство 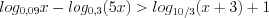 .
.
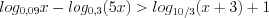 .
.Решение. ОДЗ: 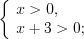
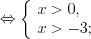
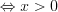 .
.
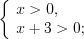
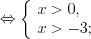
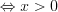 .
.Применяя свойства логарифмов, запишем неравенство в виде:
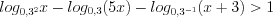 ,
,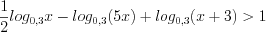 ,
,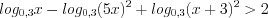 ,
, 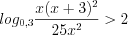 .
. Поскольку основание логарифма 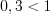 , то
, то 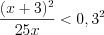 , а так как
, а так как 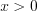 , то запишем:
, то запишем: 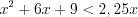 ,
, 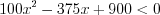 . Так как
. Так как 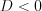 , то это неравенство решений не имеет.
, то это неравенство решений не имеет.
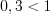 , то
, то 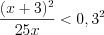 , а так как
, а так как 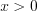 , то запишем:
, то запишем: 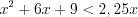 ,
, 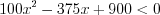 . Так как
. Так как 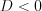 , то это неравенство решений не имеет.
, то это неравенство решений не имеет.Ответ: 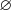 .
.
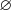 .
.Пример 5. Найдите наименьшее натуральное число, которое не является решением неравенства 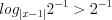 .
.
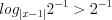 .
.1. Рассмотрим функцию 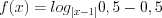 .
.
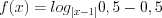 .
.2. 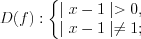
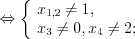
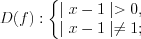
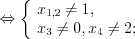
3. Найдем нули функции, решая уравнение 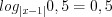 , откуда
, откуда 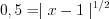 ,
, 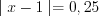 . Тогда
. Тогда 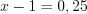 или
или 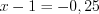 , а
, а 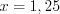 или
или 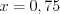 .
.
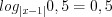 , откуда
, откуда 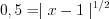 ,
, 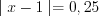 . Тогда
. Тогда 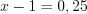 или
или 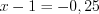 , а
, а 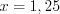 или
или 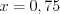 .
.4. Нанесем нули функции на ее область определения и установим знаки значений функции на полученных промежутках (рис. 7.47).
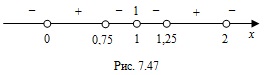
5. Решением неравенства являются промежутки, на которых функция положительна: 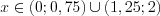 . Число 1 – наименьшее натуральное число, которое не является решением данного неравенства.
. Число 1 – наименьшее натуральное число, которое не является решением данного неравенства.
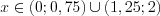 . Число 1 – наименьшее натуральное число, которое не является решением данного неравенства.
. Число 1 – наименьшее натуральное число, которое не является решением данного неравенства.Ответ: 1.
Пример 6. Найдите среднее арифметическое всех целых решений неравенства 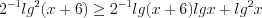 .
.
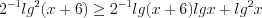 .
.Решение. ОДЗ: 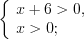
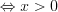 .
.
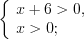
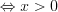 .
. Запишем неравенство в виде 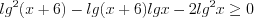 и решим его методом интервалов.
и решим его методом интервалов.
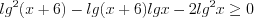 и решим его методом интервалов.
и решим его методом интервалов. По теореме, обратной теореме Виета, найдем нули функции 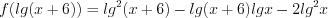 .
.
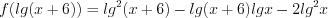 .
. 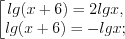
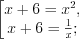

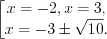
Согласно рисунку 7.48 запишем его решение:  .
.
 .
.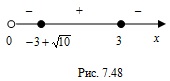
Запишем целые решения неравенства: 1; 2; 3. Найдем среднее арифметическое этих решений: 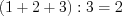 .
.
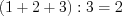 .
.Ответ: 2.
Пример 7. Решите неравенство  .
.
 .
.Решение. Запишем неравенство в виде 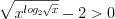 и решим его методом интервалов.
и решим его методом интервалов.
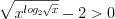 и решим его методом интервалов.
и решим его методом интервалов.1. Рассмотрим функцию 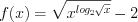 .
.
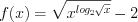 .
.2. 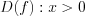 ,
,
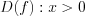 ,
,3. Найдем нули функции, решая уравнение 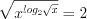 . Возводя обе части уравнения дважды в квадрат, получим
. Возводя обе части уравнения дважды в квадрат, получим 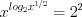 ,
, 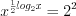 ,
, 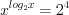 . Полагая
. Полагая  , а
, а 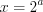 , запишем
, запишем 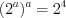 ,
,  . Тогда
. Тогда 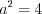 и
и 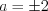 . В таком случае
. В таком случае 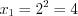 и
и  .
.
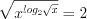 . Возводя обе части уравнения дважды в квадрат, получим
. Возводя обе части уравнения дважды в квадрат, получим 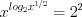 ,
, 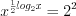 ,
, 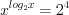 . Полагая
. Полагая  , а
, а 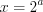 , запишем
, запишем 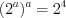 ,
,  . Тогда
. Тогда 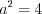 и
и 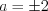 . В таком случае
. В таком случае 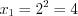 и
и  .
.4. Нанесем нули функции на ее область определения и установим знаки ее значений на полученных промежутках (рис. 7.49).

5. Решением неравенства являются промежутки, на которых функция положительна.
Ответ: 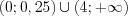 .
.
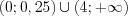 .
.Пример 8. Найдите область определения функции 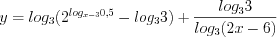 .
.
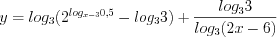 .
.Решение. Найдем область определения функции, решая систему ограничений: 
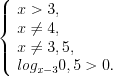

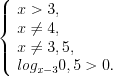
Рассмотрим решение неравенства 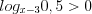 на промежутках
на промежутках 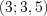 ,
, 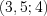 и
и 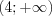 .
.
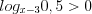 на промежутках
на промежутках 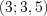 ,
, 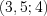 и
и 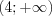 .
.Поскольку функция 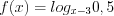 нулей не имеет, то установим знаки ее значений на указанных промежутках (рис. 7.50).
нулей не имеет, то установим знаки ее значений на указанных промежутках (рис. 7.50).
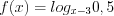 нулей не имеет, то установим знаки ее значений на указанных промежутках (рис. 7.50).
нулей не имеет, то установим знаки ее значений на указанных промежутках (рис. 7.50).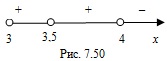
Согласно рисунку 7.50 решением системы неравенств являются промежутки, на которых функция положительна.
Ответ: 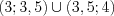 .
.
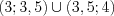 .
.Пример 9. Найдите решение неравенства 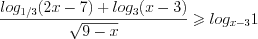 .
.
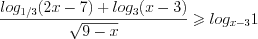 .
.Решение. Запишем данное неравенство в виде 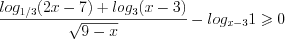 и решим его методом интервалов.
и решим его методом интервалов.
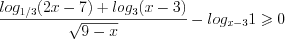 и решим его методом интервалов.
и решим его методом интервалов.1. Рассмотрим функцию 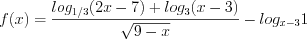 .
.
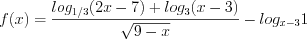 .
.2. 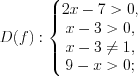
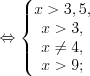
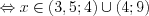 .
.
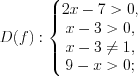
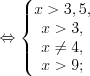
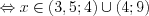 .
.3. На области определения функция примет вид: 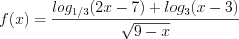 .
.
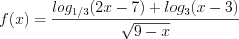 .
.Найдем её нули, решая уравнение: 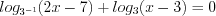 ,
, 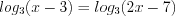 ,
, 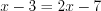 ,
, 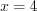 .
.
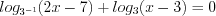 ,
, 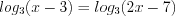 ,
, 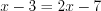 ,
, 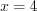 .
.4. Поскольку значение 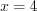 не принадлежит области определения функции, то установим знаки функции на ее области определения (рис. 7.51).
не принадлежит области определения функции, то установим знаки функции на ее области определения (рис. 7.51).
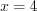 не принадлежит области определения функции, то установим знаки функции на ее области определения (рис. 7.51).
не принадлежит области определения функции, то установим знаки функции на ее области определения (рис. 7.51).
5. Решением неравенства является промежуток, на котором функция не отрицательна.
Ответ: 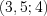 .
.
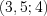 .
. Пример 10. Найдите наименьшее целое решение неравенства 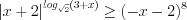 .
.
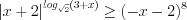 .
.Решение. Поскольку 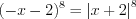 , то запишем неравенство в виде
, то запишем неравенство в виде 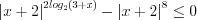 и решим его методом интервалов.
и решим его методом интервалов.
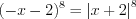 , то запишем неравенство в виде
, то запишем неравенство в виде 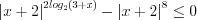 и решим его методом интервалов.
и решим его методом интервалов.1. Рассмотрим функцию 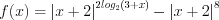 .
.
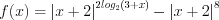 .
.2. 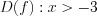 .
.
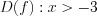 .
.3. Найдем нули функции, решая уравнение 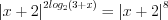 :
:
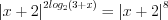 :
:1)  , откуда
, откуда 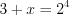 и
и 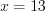 ;
;
 , откуда
, откуда 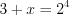 и
и 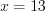 ;
; 2) 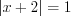
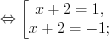
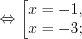
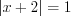
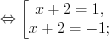
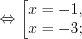
3) 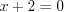 , откуда
, откуда 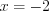 . Проверка: подставляя значение
. Проверка: подставляя значение 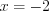 в уравнение
в уравнение 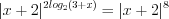 , получим
, получим 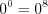 . Поскольку получили неопределенность вида
. Поскольку получили неопределенность вида 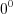 , то
, то 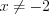 .
.
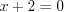 , откуда
, откуда 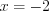 . Проверка: подставляя значение
. Проверка: подставляя значение 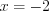 в уравнение
в уравнение 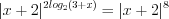 , получим
, получим 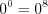 . Поскольку получили неопределенность вида
. Поскольку получили неопределенность вида 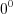 , то
, то 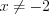 .
.4. Нанесем нули функции на ее область определения и установим знаки ее значений на полученных промежутках (рис.7.52).

5. Решением неравенства является объединение промежутков, на которых функция не отрицательна: ![(-3;-2)\cup (-2;-1]\cup [13;+ \infty) LaTeX formula: (-3;-2)\cup (-2;-1]\cup [13;+ \infty)](/uploads/formulas/204205492f92e5b607c1c9ae7a0a1c68c176e381.1.1.png) .
.
![(-3;-2)\cup (-2;-1]\cup [13;+ \infty) LaTeX formula: (-3;-2)\cup (-2;-1]\cup [13;+ \infty)](/uploads/formulas/204205492f92e5b607c1c9ae7a0a1c68c176e381.1.1.png) .
. Число  – наименьшее целое решение неравенства.
– наименьшее целое решение неравенства.
 – наименьшее целое решение неравенства.
– наименьшее целое решение неравенства.Ответ:  .
.
 .
.Всякое логарифмическое неравенство можно решить методом интервалов, но наиболее целесообразно этот метод применять в случае решения неравенств 7.19 и комбинированных неравенств.


 равносильно
равносильно