Справочный материал
Примеры
Обратите внимание!
Видео
Модели
Пройти тесты
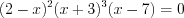 .
.

![(-2;1]\cup (2;+\infty )\cup \left \{ 0 \right \} LaTeX formula: (-2;1]\cup (2;+\infty )\cup \left \{ 0 \right \}](/uploads/formulas/e685e1500d083500f5d5ac42f09bbecd8da6ce82.1.1.png) .
.
 ,
, 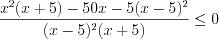 ,
, 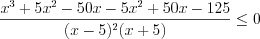 ,
, 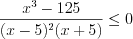 .
.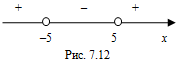

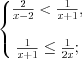
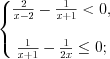
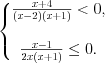
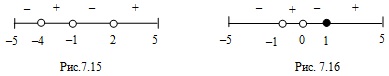


Целым рациональным неравенством называют неравенство вида 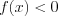 (>, ≤, ≥), где
(>, ≤, ≥), где  – алгебраический многочлен.
– алгебраический многочлен.
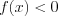 (>, ≤, ≥), где
(>, ≤, ≥), где  – алгебраический многочлен.
– алгебраический многочлен. Дробным рациональным неравенством называют неравенство вида 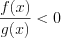 (>, ≤, ≥), где
(>, ≤, ≥), где  и
и  – алгебраические многочлены. Очевидно, что множество решений дробно-рационального неравенства не должно содержать корней многочлена
– алгебраические многочлены. Очевидно, что множество решений дробно-рационального неравенства не должно содержать корней многочлена  .
.
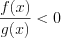 (>, ≤, ≥), где
(>, ≤, ≥), где  и
и  – алгебраические многочлены. Очевидно, что множество решений дробно-рационального неравенства не должно содержать корней многочлена
– алгебраические многочлены. Очевидно, что множество решений дробно-рационального неравенства не должно содержать корней многочлена  .
. Рассмотрим дробно-рациональную функцию 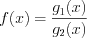 . Корни многочлена
. Корни многочлена 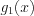 называют нулями функции, а корни многочлена
называют нулями функции, а корни многочлена 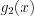 называют точками разрыва функции.
называют точками разрыва функции.
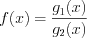 . Корни многочлена
. Корни многочлена 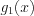 называют нулями функции, а корни многочлена
называют нулями функции, а корни многочлена 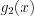 называют точками разрыва функции.
называют точками разрыва функции. Решая дробно-рациональное неравенство 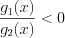 (>, ≤, ≥) методом интервалов можно не находить область определения функции
(>, ≤, ≥) методом интервалов можно не находить область определения функции 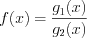 , а нанести на координатную прямую ее нули и точки разрыва и определить знаки значений функции на полученных промежутках.
, а нанести на координатную прямую ее нули и точки разрыва и определить знаки значений функции на полученных промежутках.
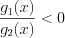 (>, ≤, ≥) методом интервалов можно не находить область определения функции
(>, ≤, ≥) методом интервалов можно не находить область определения функции 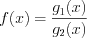 , а нанести на координатную прямую ее нули и точки разрыва и определить знаки значений функции на полученных промежутках.
, а нанести на координатную прямую ее нули и точки разрыва и определить знаки значений функции на полученных промежутках. Пример 1. Решите неравенство 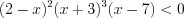 .
.
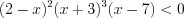 .
.Решение. 1. Рассмотрим функцию 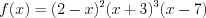 .
.
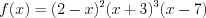 .
.2. Найдем нули функции, решая уравнение
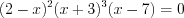 .
.Получим 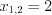 ,
, 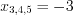 ,
, 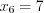 .
.
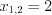 ,
, 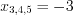 ,
, 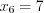 .
.3. Корни нечетной кратности –3 и 7 нанесем на координатную прямую один раз, а корень четной кратности 2 – два раза (рис. 7.8).
Определим знаки значений функции на любом промежутке, например, на промежутке 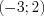 , найдя значение функции в точке
, найдя значение функции в точке  , принадлежащей этому промежутку:
, принадлежащей этому промежутку: 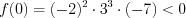 .
.
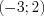 , найдя значение функции в точке
, найдя значение функции в точке  , принадлежащей этому промежутку:
, принадлежащей этому промежутку: 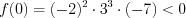 .
.
Определим знаки значений функции на остальных промежутках, чередуя их при переходе через точки –3 и 7 и сохраняя знак (чередуя дважды) при переходе через точку 2.
4. Объединив промежутки, на которых функция отрицательна, получим решение данного неравенства: 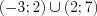 .
.
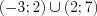 .
.Ответ: 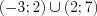 .
.
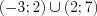 .
.Пример 2. Решите неравенство 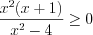 .
.
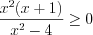 .
.Решение. 1. Рассмотрим функцию 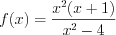 .
.
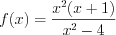 .
.2. Найдем нули функции, решая уравнение 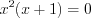 . Получим
. Получим 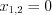 ,
, 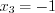 . Найдем точки разрыва функции, решая уравнение
. Найдем точки разрыва функции, решая уравнение 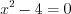 . Получим
. Получим 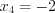 ,
, 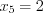 .
.
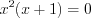 . Получим
. Получим 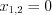 ,
, 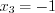 . Найдем точки разрыва функции, решая уравнение
. Найдем точки разрыва функции, решая уравнение 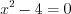 . Получим
. Получим 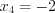 ,
, 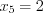 .
. 3. Нанесем нули и точки разрыва функции на координатную прямую, при этом точки разрыва отметим на координатной прямой «пустыми» кружочками, а нули функции «зачерненными» кружочками (рис. 7.9). Определим знаки значений функции на полученных промежутках.

4. Так как функция 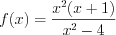 может быть как положительной, так и равной нулю (на это указывает смысловой знак неравенства
может быть как положительной, так и равной нулю (на это указывает смысловой знак неравенства  ), то решением неравенства является объединение промежутков, на которых функция неотрицательна и число
), то решением неравенства является объединение промежутков, на которых функция неотрицательна и число  :
:
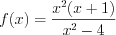 может быть как положительной, так и равной нулю (на это указывает смысловой знак неравенства
может быть как положительной, так и равной нулю (на это указывает смысловой знак неравенства  ), то решением неравенства является объединение промежутков, на которых функция неотрицательна и число
), то решением неравенства является объединение промежутков, на которых функция неотрицательна и число  :
: ![(-2;1]\cup (2;+\infty )\cup \left \{ 0 \right \} LaTeX formula: (-2;1]\cup (2;+\infty )\cup \left \{ 0 \right \}](/uploads/formulas/e685e1500d083500f5d5ac42f09bbecd8da6ce82.1.1.png) .
.Ответ: ![(-2;1]\cup (2;+\infty )\cup \left \{ 0 \right \} LaTeX formula: (-2;1]\cup (2;+\infty )\cup \left \{ 0 \right \}](http://helpy.quali.me/uploads/formulas/e685e1500d083500f5d5ac42f09bbecd8da6ce82.1.1.png) .
.
![(-2;1]\cup (2;+\infty )\cup \left \{ 0 \right \} LaTeX formula: (-2;1]\cup (2;+\infty )\cup \left \{ 0 \right \}](http://helpy.quali.me/uploads/formulas/e685e1500d083500f5d5ac42f09bbecd8da6ce82.1.1.png) .
.Пример 3. Решите неравенство 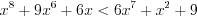 .
.
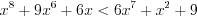 .
.Решение. Запишем неравенство в виде 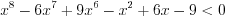 и разложим его левую часть на множители:
и разложим его левую часть на множители: 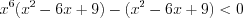 ,
, 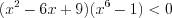 ,
, 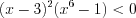 .
.
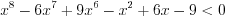 и разложим его левую часть на множители:
и разложим его левую часть на множители: 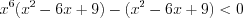 ,
, 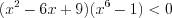 ,
, 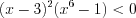 .
.1. Рассмотрим функцию 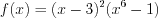 .
.
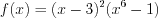 .
.2. Найдем нули функции, решая уравнение 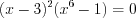 , равносильное совокупности уравнений
, равносильное совокупности уравнений 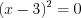 и
и 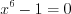 . Получим
. Получим 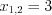 ,
, 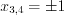 .
.
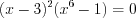 , равносильное совокупности уравнений
, равносильное совокупности уравнений 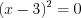 и
и 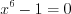 . Получим
. Получим 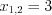 ,
, 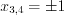 .
.3. Нанесем нули функции на координатную прямую (рис. 7.10) и определим знаки функции на полученных промежутках.

4. Решением неравенства является промежуток, на котором функция 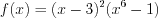 отрицательна:
отрицательна: 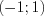 .
.
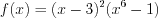 отрицательна:
отрицательна: 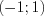 .
.Ответ: 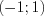 .
.
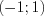 .
.Пример 4. Решите неравенство 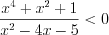 .
.
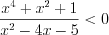 .
. Решение. 1. Рассмотрим функцию 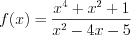 .
.
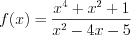 .
.2. Найдем нули функции, решая уравнение 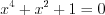 . Поскольку
. Поскольку  , то уравнение не имеет действительных корней. Найдем точки разрыва функции, решая уравнение
, то уравнение не имеет действительных корней. Найдем точки разрыва функции, решая уравнение 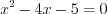 , откуда
, откуда 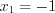 и
и 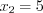 .
.
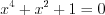 . Поскольку
. Поскольку  , то уравнение не имеет действительных корней. Найдем точки разрыва функции, решая уравнение
, то уравнение не имеет действительных корней. Найдем точки разрыва функции, решая уравнение 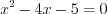 , откуда
, откуда 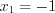 и
и 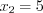 .
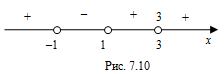
.3. Нанесем числа –1 и 5 на координатную прямую и определим знаки значений функции на полученных промежутках (рис. 7.11).

4. Решением неравенства является промежуток, на котором функция 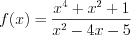 отрицательна:
отрицательна: 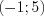 .
.
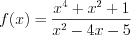 отрицательна:
отрицательна: 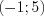 .
.Ответ: 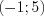 .
.
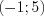 .
. Пример 5. Определите количество целых решений неравенства 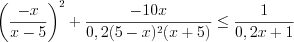 .
.
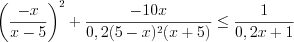 .
.Решение. Запишем неравенство в виде 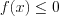 :
:
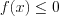 :
: 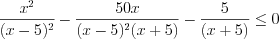 ,
,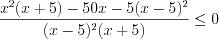 ,
, 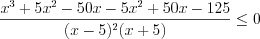 ,
, 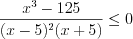 .
.1. Рассмотрим функцию 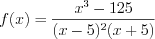 .
.
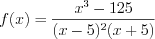 .
.2. Найдем нули функции, решая уравнение 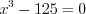 , откуда
, откуда 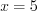 . Найдем точки разрыва функции, решая уравнения
. Найдем точки разрыва функции, решая уравнения 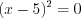 , откуда
, откуда 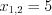 и
и 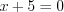 , откуда
, откуда 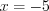 .
.
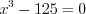 , откуда
, откуда 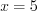 . Найдем точки разрыва функции, решая уравнения
. Найдем точки разрыва функции, решая уравнения 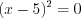 , откуда
, откуда 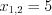 и
и 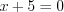 , откуда
, откуда 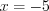 .
.3. Нанесем полученные числа на координатную прямую (рис. 7.12) и определим знак значений функции 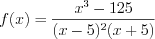 на промежутке
на промежутке 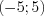 , подставив в функцию любое число из указанного промежутка, например, число 0:
, подставив в функцию любое число из указанного промежутка, например, число 0: 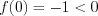 . Определим знак значений функции на остальных промежутках, чередуя их при переходе через точки 5 и –5 (числа 5 и –5 – корни нечетной кратности).
. Определим знак значений функции на остальных промежутках, чередуя их при переходе через точки 5 и –5 (числа 5 и –5 – корни нечетной кратности).
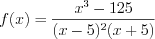 на промежутке
на промежутке 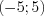 , подставив в функцию любое число из указанного промежутка, например, число 0:
, подставив в функцию любое число из указанного промежутка, например, число 0: 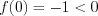 . Определим знак значений функции на остальных промежутках, чередуя их при переходе через точки 5 и –5 (числа 5 и –5 – корни нечетной кратности).
. Определим знак значений функции на остальных промежутках, чередуя их при переходе через точки 5 и –5 (числа 5 и –5 – корни нечетной кратности).4. Так как функция не положительна, то решением исходного неравенства является интервал 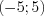 (рис. 7.12).
(рис. 7.12).
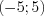 (рис. 7.12).
(рис. 7.12).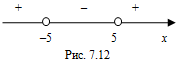
Запишем целые решения неравенства: 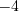 ,
, 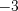 ,
, 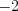 ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  .
.
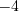 ,
, 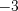 ,
, 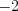 ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  .
.Ответ: 9.
Пример 6. Найдите среднее арифметическое целых решений неравенства 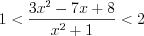 .
.
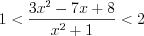 .
.Решение. Данное неравенство равносильно системе неравенств 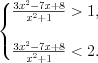 Решим каждое неравенство системы методом интервалов, предварительно умножив эти неравенства на
Решим каждое неравенство системы методом интервалов, предварительно умножив эти неравенства на 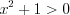 .
.
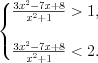 Решим каждое неравенство системы методом интервалов, предварительно умножив эти неравенства на
Решим каждое неравенство системы методом интервалов, предварительно умножив эти неравенства на 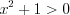 .
.1. Первое неравенство примет вид 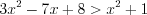 или
или 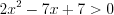 . Оно справедливо для любых
. Оно справедливо для любых 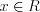 , так как график квадратичной функции
, так как график квадратичной функции 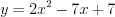 не пересекает ось абсцисс (D < 0) и ветви параболы направлены вверх.
не пересекает ось абсцисс (D < 0) и ветви параболы направлены вверх.
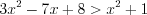 или
или 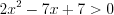 . Оно справедливо для любых
. Оно справедливо для любых 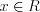 , так как график квадратичной функции
, так как график квадратичной функции 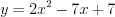 не пересекает ось абсцисс (D < 0) и ветви параболы направлены вверх.
не пересекает ось абсцисс (D < 0) и ветви параболы направлены вверх.2. Второе неравенство примет вид 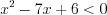 . Его решение:
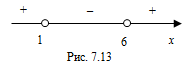
. Его решение: 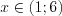 (рис. 7.13).
(рис. 7.13).
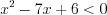 . Его решение:
. Его решение: 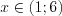 (рис. 7.13).
(рис. 7.13).
Поскольку решение второго неравенства является подмножеством решений первого, то интервал 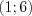 является решением исходной системы неравенств. Запишем целые решения системы неравенств: 2, 3, 4, 5. Найдем среднее арифметическое этих чисел:
является решением исходной системы неравенств. Запишем целые решения системы неравенств: 2, 3, 4, 5. Найдем среднее арифметическое этих чисел: 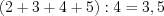 .
.
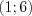 является решением исходной системы неравенств. Запишем целые решения системы неравенств: 2, 3, 4, 5. Найдем среднее арифметическое этих чисел:
является решением исходной системы неравенств. Запишем целые решения системы неравенств: 2, 3, 4, 5. Найдем среднее арифметическое этих чисел: 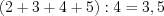 .
.Ответ: 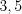 .
.
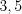 .
.Пример 7. Найдите сумму целых решений системы неравенств 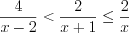 , удовлетворяющих условию
, удовлетворяющих условию 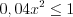 .
.
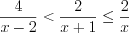 , удовлетворяющих условию
, удовлетворяющих условию 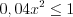 .
. Решение. Запишем неравенство 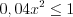 в виде
в виде 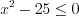 ,
, 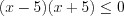 и решим его методом интервалов.
и решим его методом интервалов.
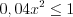 в виде
в виде 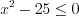 ,
, 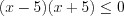 и решим его методом интервалов.
и решим его методом интервалов. Согласно рисунку 7.14 запишем его решение: ![x\in \left [ -5;5 \right ] LaTeX formula: x\in \left [ -5;5 \right ]](/uploads/formulas/99524cc9c1d694b5238357490bd124dda3b0c495.1.1.png) .
.
![x\in \left [ -5;5 \right ] LaTeX formula: x\in \left [ -5;5 \right ]](/uploads/formulas/99524cc9c1d694b5238357490bd124dda3b0c495.1.1.png) .
.
Решим систему неравенств 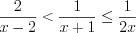 на отрезке
на отрезке ![\left [ -5;5 \right ] LaTeX formula: \left [ -5;5 \right ]](/uploads/formulas/dc38cd34c0a5816dd6c2de9fc55bf2c5ba2e0421.1.1.png) :
:
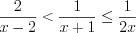 на отрезке
на отрезке ![\left [ -5;5 \right ] LaTeX formula: \left [ -5;5 \right ]](/uploads/formulas/dc38cd34c0a5816dd6c2de9fc55bf2c5ba2e0421.1.1.png) :
: 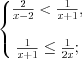
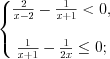
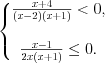
Решение первого неравенства системы показано на рисунке 7.15: 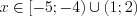 .
.
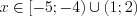 .
.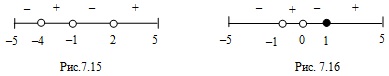
Решение второго неравенства системы показано на рисунке 7.16: ![x\in \left [ -5;-1)\cup (0;1] LaTeX formula: x\in \left [ -5;-1)\cup (0;1]](/uploads/formulas/295c155674bf88434802fcfb0caabd39c63eb4ed.1.1.png) .
.
![x\in \left [ -5;-1)\cup (0;1] LaTeX formula: x\in \left [ -5;-1)\cup (0;1]](/uploads/formulas/295c155674bf88434802fcfb0caabd39c63eb4ed.1.1.png) .
.Решение системы неравенств показано на рисунке 7.17: ![x\in \left [ -5;4)\cup (0;1] LaTeX formula: x\in \left [ -5;4)\cup (0;1]](/uploads/formulas/b3f81f2aae4f355cf3f9fb759745d411858123c5.1.1.png) .
.
![x\in \left [ -5;4)\cup (0;1] LaTeX formula: x\in \left [ -5;4)\cup (0;1]](/uploads/formulas/b3f81f2aae4f355cf3f9fb759745d411858123c5.1.1.png) .
.
Исходная система неравенств имеет два целых решения, удовлетворяющих условию 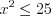 . Найдем сумму этих решений:
. Найдем сумму этих решений: 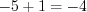 .
.
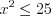 . Найдем сумму этих решений:
. Найдем сумму этих решений: 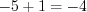 .
.Ответ: 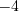 .
.
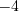 .
. Пример 8. Найдите область определения функции 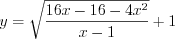 .
.
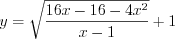 .
.Решение. Имеем иррациональную функцию четной степени корня. Следовательно, выражение, стоящее под знаком радикала, не должно быть отрицательным: 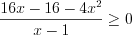 или
или 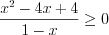 ,
, 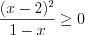 .
.
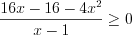 или
или 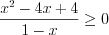 ,
, 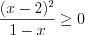 .
. Решим полученное неравенство методом интервалов.
1. Рассмотрим функцию 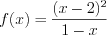 .
.
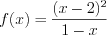 .
.2. Найдем нули функции, решая уравнение 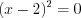 , откуда
, откуда 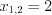 . Найдем точки разрыва функции, решая уравнение
. Найдем точки разрыва функции, решая уравнение 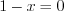 , откуда
, откуда  .
.
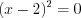 , откуда
, откуда 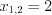 . Найдем точки разрыва функции, решая уравнение
. Найдем точки разрыва функции, решая уравнение 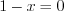 , откуда
, откуда  .
.3. Нанесем нули и точки разрыва функции на координатную прямую и определим знаки значений функции на полученных промежутках (рис. 7.18).

4. Решением неравенства является промежуток 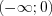 , на котором функция
, на котором функция 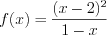 положительна, и точка 2, в которой функция обращается в нуль.
положительна, и точка 2, в которой функция обращается в нуль.
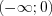 , на котором функция
, на котором функция 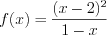 положительна, и точка 2, в которой функция обращается в нуль.
положительна, и точка 2, в которой функция обращается в нуль.Ответ: 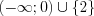 .
.
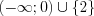 .
.Сравните решения неравенств:
1) неравенство 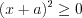 выполняется при
выполняется при 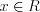 ;
;
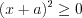 выполняется при
выполняется при 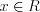 ;
; 2) неравенство 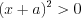 выполняется при
выполняется при 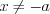 ;
;
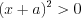 выполняется при
выполняется при 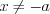 ;
;3) неравенство 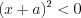 решений не имеет;
решений не имеет;
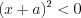 решений не имеет;
решений не имеет;4) неравенство 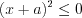 имеет единственное решение
имеет единственное решение 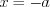 .
.
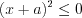 имеет единственное решение
имеет единственное решение 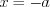 .
.
