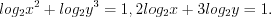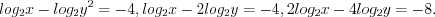Справочный материал
Примеры
Обратите внимание!
Видео
Модели
Пройти тесты
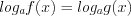 , (5.18)
, (5.18) (5.18.1)
(5.18.1)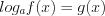 , (5.19)
, (5.19)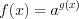 (5.19.1)
(5.19.1)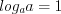 ; (3.15)
; (3.15)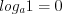 ; (3.16)
; (3.16)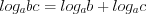 ; (3.17)
; (3.17)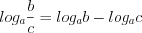 ; (3.18)
; (3.18)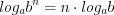 ; (3.19)
; (3.19)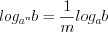 ; (3.20)
; (3.20)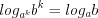 ; (3.21)
; (3.21)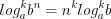 ; (3.22)
; (3.22)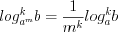 ; (3.23)
; (3.23)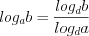 ; (3.24)
; (3.24)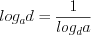 ; (3.25)
; (3.25)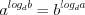 . (3.26)
. (3.26)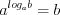 . (3.27)
. (3.27)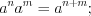
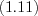
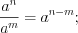
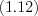
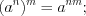

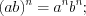
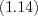
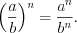
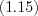
 .
.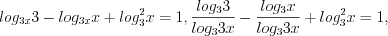
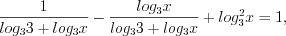
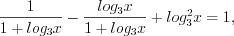
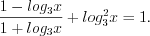
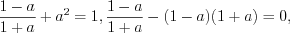
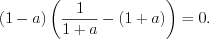
Логарифмическими называют уравнения, содержащие переменную под знаком логарифма, например, уравнения вида: 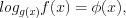 где
где 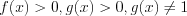 .
.
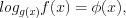 где
где 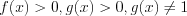 .
.Методы решений уравнений
1. Если уравнение имеет вид
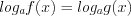 , (5.18)
, (5.18)то оно равносильно уравнению
 (5.18.1)
(5.18.1)при условии, что  и
и 

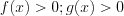 .
.
 и
и 

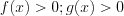 .
. 2. Если уравнение имеет вид
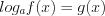 , (5.19)
, (5.19)то оно равносильно уравнению
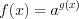 (5.19.1)
(5.19.1)при условии, что  и
и  .
.
 и
и  .
. 3. Метод подстановки.
4. Использование монотонности функций.
Свойства логарифмов:
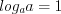 ; (3.15)
; (3.15)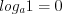 ; (3.16)
; (3.16)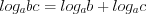 ; (3.17)
; (3.17)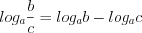 ; (3.18)
; (3.18)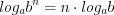 ; (3.19)
; (3.19)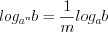 ; (3.20)
; (3.20)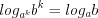 ; (3.21)
; (3.21)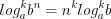 ; (3.22)
; (3.22)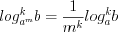 ; (3.23)
; (3.23)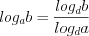 ; (3.24)
; (3.24)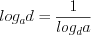 ; (3.25)
; (3.25)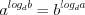 . (3.26)
. (3.26)Свойства 3.15 – 3.26 справедливы при  и
и 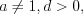 и
и 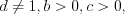 причем числа
причем числа 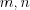 и
и  отличны от нуля.
отличны от нуля.
 и
и 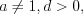 и
и 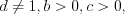 причем числа
причем числа 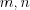 и
и  отличны от нуля.
отличны от нуля. Основное логарифмическое тождество:
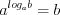 . (3.27)
. (3.27)Свойства степеней:
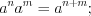
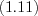
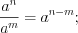
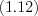
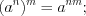

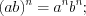
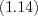
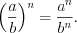
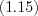
Пример 1. Найдите квадрат десятичного логарифма суммы корней (или корня, если он единственный) уравнения 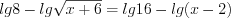 .
.
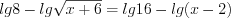 .
.Решение. ОДЗ: 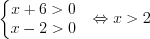 .
.
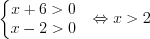 .
.Имеем уравнение вида 5.18, которое равносильно уравнению 5.18.1. Тогда: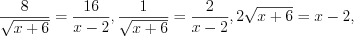

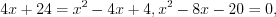
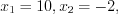 причем число
причем число 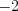 – посторонний корень уравнения. Тогда
– посторонний корень уравнения. Тогда 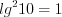 .
.
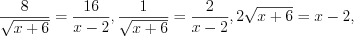

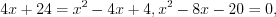
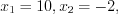 причем число
причем число 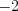 – посторонний корень уравнения. Тогда
– посторонний корень уравнения. Тогда 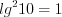 .
.Ответ:  .
.
 .
.Пример 2. Решите уравнение
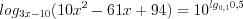 .
.Решение. ОДЗ: 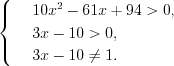
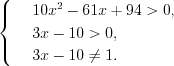
Так как имеем уравнение вида 5.19 , то исходное уравнение на ОДЗ равносильно уравнению 5.19.1, то 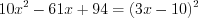 или
или 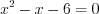 , откуда
, откуда 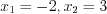 . Поскольку числа
. Поскольку числа 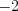 и
и  не принадлежат области допустимых значений уравнения, то уравнение корней не имеет.
не принадлежат области допустимых значений уравнения, то уравнение корней не имеет.
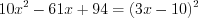 или
или 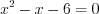 , откуда
, откуда 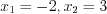 . Поскольку числа
. Поскольку числа 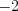 и
и  не принадлежат области допустимых значений уравнения, то уравнение корней не имеет.
не принадлежат области допустимых значений уравнения, то уравнение корней не имеет.Ответ:  .
.
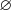 .
.Пример 3. Решите уравнение 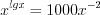 .
.
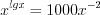 .
.Решение. ОДЗ: 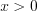 . Полагая
. Полагая 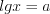 , запишем
, запишем 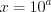 и решим показательное уравнение
и решим показательное уравнение 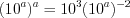 .
.
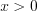 . Полагая
. Полагая 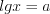 , запишем
, запишем 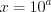 и решим показательное уравнение
и решим показательное уравнение 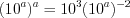 .
. Учитывая подстановку, найдем корни исходного уравнения: 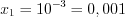 и
и 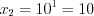 .
.
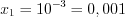 и
и 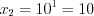 .
.Ответ: 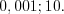
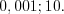
Пример 4. Найдите среднее геометрическое корней уравнения 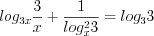 .
.
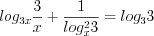 .
.Решение. ОДЗ: 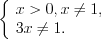
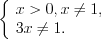
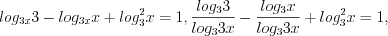
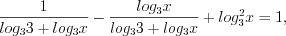
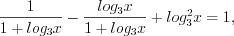
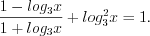
В результате подстановки 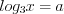 получим:
получим:
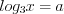 получим:
получим: 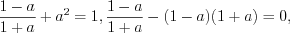
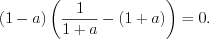
Решим два уравнения: 1) 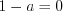 , откуда
, откуда 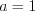 ;
;
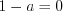 , откуда
, откуда 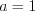 ;
; 2) 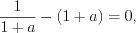 откуда
откуда 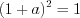 и
и  или
или 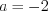 .
.
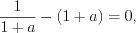 откуда
откуда 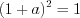 и
и  или
или 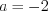 .
.Учитывая подстановку, решим уравнения:
1) 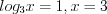 ;
;
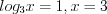 ;
;2) 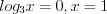 – посторонний корень;
– посторонний корень;
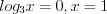 – посторонний корень;
– посторонний корень;3) 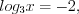
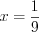 .
.
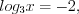
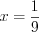 .
.Найдем среднее геометрическое корней уравнения: 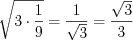 .
.
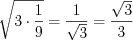 .
.Ответ: 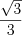 .
.
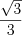 .
.Пример 5. Решите систему уравнений 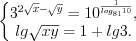
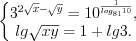
Решение. ОДЗ: 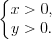
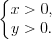
Запишем систему уравнений в виде 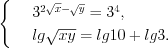
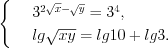
Рассматриваемая система состоит из показательного и логарифмического уравнений и равносильна системе 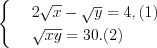
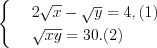
Выразим 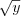 из уравнения (1):
из уравнения (1): 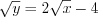 . Подставим полученное выражение в уравнение (2):
. Подставим полученное выражение в уравнение (2): 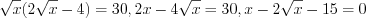 . Получили квадратное уравнение относительно
. Получили квадратное уравнение относительно 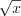 . Значит
. Значит 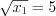 , откуда
, откуда 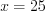 и
и 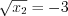 , откуда
, откуда  .
.
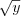 из уравнения (1):
из уравнения (1): 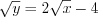 . Подставим полученное выражение в уравнение (2):
. Подставим полученное выражение в уравнение (2): 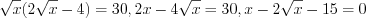 . Получили квадратное уравнение относительно
. Получили квадратное уравнение относительно 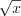 . Значит
. Значит 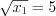 , откуда
, откуда 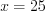 и
и 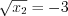 , откуда
, откуда  .
.Найдем  :
: 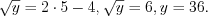
 :
: 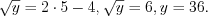
Ответ: 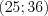 .
.
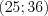 .
.Пример 6. Найдите произведение чисел  и
и  , если
, если 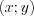 – решение системы уравнений
– решение системы уравнений 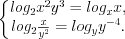
 и
и  , если
, если 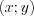 – решение системы уравнений
– решение системы уравнений 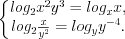
Решение. ОДЗ: 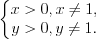
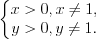
Найдем разность левых и правых частей полученных уравнений: 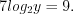
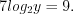
Тогда 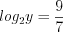 , а
, а 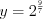 .
.
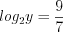 , а
, а 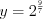 .
. Найдем значение  из уравнения
из уравнения 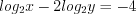 . Получим:
. Получим: 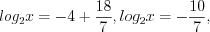 откуда
откуда 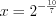 .
.
 из уравнения
из уравнения 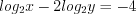 . Получим:
. Получим: 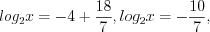 откуда
откуда 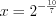 .
. Найдем произведение полученных значений  и
и  :
: ![xy=2^{-\frac{10}{7}}\cdot 2^{\frac{9}{7}}=2^{-\frac{1}{7}}=\sqrt[7]{0,5} . LaTeX formula: xy=2^{-\frac{10}{7}}\cdot 2^{\frac{9}{7}}=2^{-\frac{1}{7}}=\sqrt[7]{0,5} .](/uploads/formulas/bccd9be32a47dd844f48883904a4809b70c4e448.1.1.png)
 и
и  :
: ![xy=2^{-\frac{10}{7}}\cdot 2^{\frac{9}{7}}=2^{-\frac{1}{7}}=\sqrt[7]{0,5} . LaTeX formula: xy=2^{-\frac{10}{7}}\cdot 2^{\frac{9}{7}}=2^{-\frac{1}{7}}=\sqrt[7]{0,5} .](/uploads/formulas/bccd9be32a47dd844f48883904a4809b70c4e448.1.1.png)
Ответ: ![\sqrt[7]{0,5} LaTeX formula: \sqrt[7]{0,5}](/uploads/formulas/924cda732c2d7ad0e912ad46ae0400a21bc83c45.1.1.png) .
.
![\sqrt[7]{0,5} LaTeX formula: \sqrt[7]{0,5}](/uploads/formulas/924cda732c2d7ad0e912ad46ae0400a21bc83c45.1.1.png) .
.Пример 7. Найдите решения системы уравнений ![\left\{ \begin{array}{lcl} \sqrt[6]{x^{x+y}}=y^2,\\ \sqrt[3]{y^{x+y}}=x\\ \end{array} \right. LaTeX formula: \left\{ \begin{array}{lcl} \sqrt[6]{x^{x+y}}=y^2,\\ \sqrt[3]{y^{x+y}}=x\\ \end{array} \right.](/uploads/formulas/7c81d1b4d5970cc7105f81c48b3a44bda3e179b0.1.1.png) при условии, что
при условии, что 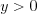 .
.
![\left\{ \begin{array}{lcl} \sqrt[6]{x^{x+y}}=y^2,\\ \sqrt[3]{y^{x+y}}=x\\ \end{array} \right. LaTeX formula: \left\{ \begin{array}{lcl} \sqrt[6]{x^{x+y}}=y^2,\\ \sqrt[3]{y^{x+y}}=x\\ \end{array} \right.](/uploads/formulas/7c81d1b4d5970cc7105f81c48b3a44bda3e179b0.1.1.png) при условии, что
при условии, что 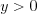 .
.Решение. Применим определение логарифма и запишем систему уравнений в виде 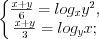
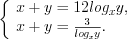
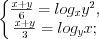
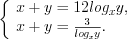
Тогда 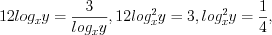 откуда
откуда 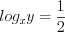 или
или 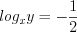 , а значит
, а значит 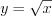 или
или 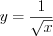 .
.
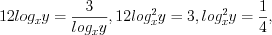 откуда
откуда 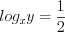 или
или 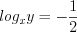 , а значит
, а значит 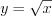 или
или 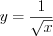 .
.Рассмотрим два случая.
1. Если 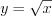 , то, подставляя значение
, то, подставляя значение  в любое уравнение исходной системы, например в уравнение
в любое уравнение исходной системы, например в уравнение 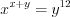 , найдем значение переменной
, найдем значение переменной  , решая показательно-степенное уравнение
, решая показательно-степенное уравнение 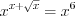 :
:
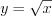 , то, подставляя значение
, то, подставляя значение  в любое уравнение исходной системы, например в уравнение
в любое уравнение исходной системы, например в уравнение 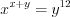 , найдем значение переменной
, найдем значение переменной  , решая показательно-степенное уравнение
, решая показательно-степенное уравнение 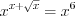 :
: 1)  откуда
откуда 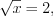 а
а 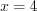 , тогда
, тогда 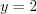 ;
;
 откуда
откуда 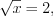 а
а 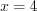 , тогда
, тогда 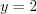 ;
; 2)  , тогда
, тогда  .
.
 , тогда
, тогда  .
.2. Если 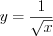 , то решим уравнение
, то решим уравнение 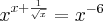 . Так как
. Так как 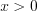 , то уравнение
, то уравнение 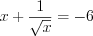 корней не имеет, а случай
корней не имеет, а случай  нами уже рассмотрен.
нами уже рассмотрен.
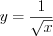 , то решим уравнение
, то решим уравнение 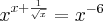 . Так как
. Так как 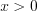 , то уравнение
, то уравнение 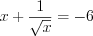 корней не имеет, а случай
корней не имеет, а случай  нами уже рассмотрен.
нами уже рассмотрен.Ответ: 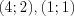 .
.
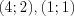 .
.1. Аргумент логарифмической функции всегда положительный, а ее основание положительное и к тому же не равно числу  .
.
 .
.2. Значение логарифма может быть положительным числом, отрицательным числом и числом  .
.
 .
.

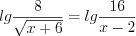 .
.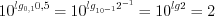 .
.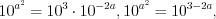 откуда
откуда 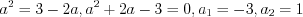 .
.