Справочный материал
Примеры
Обратите внимание!
Видео
Модели
Пройти тесты
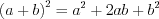 (3.1)
(3.1)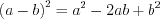 (3.2)
(3.2)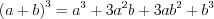 (3.3)
(3.3)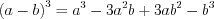 (3.4)
(3.4)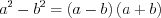 (3.5)
(3.5)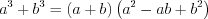 (3.6)
(3.6)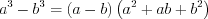 (3.7)
(3.7)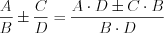 , (3.9)
, (3.9)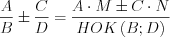 , (3.10)
, (3.10)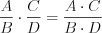 . (3.11)
. (3.11)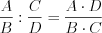 . (3.12)
. (3.12)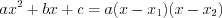 , (3.13)
, (3.13)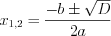 , (3.14)
, (3.14)
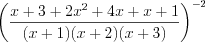
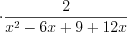
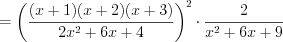
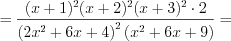
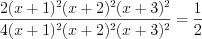 .
.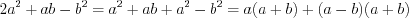
 ;
;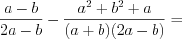

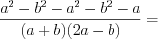
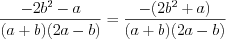 ;
;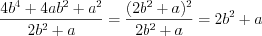 ;
;
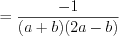 ;
;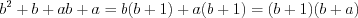 ;
;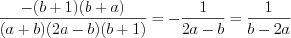 .
.
Тождеством называют равенство, верное при всех значениях переменных, принадлежащих области его определения.
Например, равенства 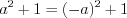 ,
,  являются тождествами, так как они справедливы на множестве всех действительных чисел.
являются тождествами, так как они справедливы на множестве всех действительных чисел.
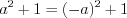 ,
,  являются тождествами, так как они справедливы на множестве всех действительных чисел.
являются тождествами, так как они справедливы на множестве всех действительных чисел.Рациональным выражением называют выражение, в котором, относительно входящих в него переменных и чисел, не выполняется никаких других операций кроме операций сложения, вычитания, умножения, деления и возведения в целую степень.
Например, выражения 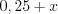 , и
, и 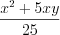 являются рациональными.
являются рациональными.
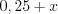 , и
, и 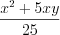 являются рациональными.
являются рациональными. Целые рациональные выражения не содержат переменную в знаменателе дроби.
Дробные рациональные выражения содержат переменную в знаменателе дроби.
Например, выражения 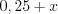 и
и 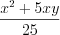 – целые, а выражение
– целые, а выражение 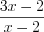 – дробное.
– дробное.
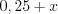 и
и 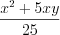 – целые, а выражение
– целые, а выражение 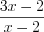 – дробное.
– дробное. Все значения переменных, при которых выражение имеет смысл, образуют область определения (или область допустимых значений) переменных выражения.
В процессе преобразований рациональных выражений используют формулы сокращенного умножения, действия с алгебраическими дробями, способы разложения многочленов на множители.
Формулы сокращенного умножения:
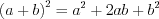 (3.1)
(3.1)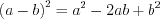 (3.2)
(3.2)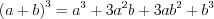 (3.3)
(3.3)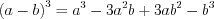 (3.4)
(3.4)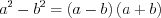 (3.5)
(3.5)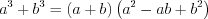 (3.6)
(3.6)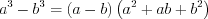 (3.7)
(3.7)Арифметические действия с алгебраическими дробями
1. Сложение (вычитание) алгебраических дробей выполняют:
а) согласно правилу:
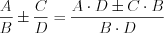 , (3.9)
, (3.9)если многочлены B и D не имеют общих множителей;
б) согласно правилу:
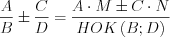 , (3.10)
, (3.10)где 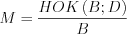 ,
, 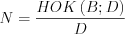 , если многочлены B и D имеют общие множители.
, если многочлены B и D имеют общие множители.
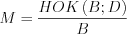 ,
, 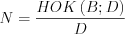 , если многочлены B и D имеют общие множители.
, если многочлены B и D имеют общие множители. Умножение алгебраических дробей выполняют согласно правилу:
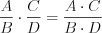 . (3.11)
. (3.11)Деление алгебраических дробей выполняют согласно правилу:
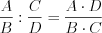 . (3.12)
. (3.12)Формула разложения квадратного трехчлена на линейные множители: 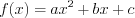 ,
,
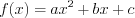 ,
,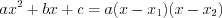 , (3.13)
, (3.13)где  и
и  – корни квадратного трехчлена.
– корни квадратного трехчлена.
 и
и  – корни квадратного трехчлена.
– корни квадратного трехчлена.Корни квадратного уравнения 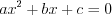 находят по формулам:
находят по формулам:
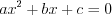 находят по формулам:
находят по формулам: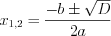 , (3.14)
, (3.14)где 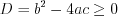 . (3.14.1)
. (3.14.1)
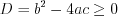 . (3.14.1)
. (3.14.1)Пример 1. Упростите выражение 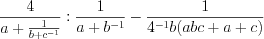 .
.
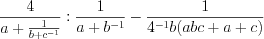 .
.1) 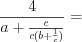
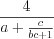
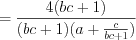
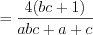 ;
;
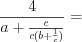
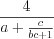
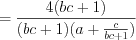
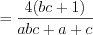 ;
;2) 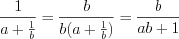 ;
;
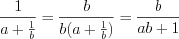 ;
;3) 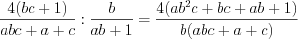 ;
;
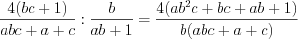 ;
;4) 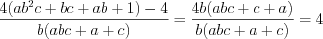 .
.
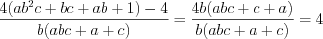 .
.Ответ: 4.
Пример 2. Упростите выражение 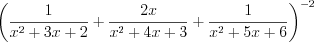
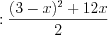 .
.
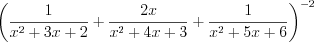
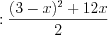 .
.Решение. Согласно правилу разложения квадратного трехчлена на линейные множители 3.13, запишем: 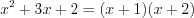 ,
, 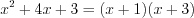 ,
, 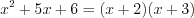 .
.
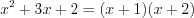 ,
, 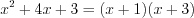 ,
, 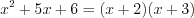 .
.Тогда исходное выражение примет вид: 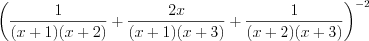 :
: 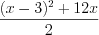 .
.
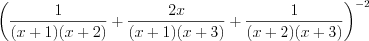 :
: 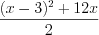 .
. Приводя дроби к общему знаменателю по правилу 3.10 и применяя формулы сокращенного умножения 3.2 и 3.1, получим:
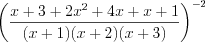
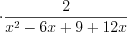
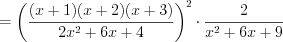
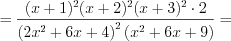
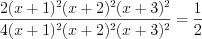 .
.Ответ: 0,5.
Пример 3. Сократите дробь 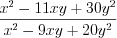 .
.
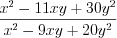 .
.Решение. Рассмотрим относительно  квадратный трехчлен
квадратный трехчлен 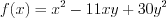 . Зная, что
. Зная, что 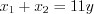 и
и  (см. теорему Виета во вкладке Обратите внимание!), получим
(см. теорему Виета во вкладке Обратите внимание!), получим 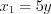 ,
, 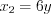 . Аналогично найдем корни квадратного трехчлена
. Аналогично найдем корни квадратного трехчлена 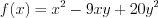 :
: 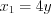 ,
, 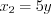 . По формуле 3.13 разложим трехчлены на линейные множители и выполним сокращение дроби:
. По формуле 3.13 разложим трехчлены на линейные множители и выполним сокращение дроби: 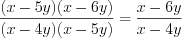 .
.
 квадратный трехчлен
квадратный трехчлен 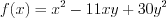 . Зная, что
. Зная, что 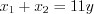 и
и  (см. теорему Виета во вкладке Обратите внимание!), получим
(см. теорему Виета во вкладке Обратите внимание!), получим 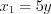 ,
, 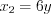 . Аналогично найдем корни квадратного трехчлена
. Аналогично найдем корни квадратного трехчлена 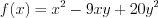 :
: 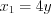 ,
, 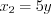 . По формуле 3.13 разложим трехчлены на линейные множители и выполним сокращение дроби:
. По формуле 3.13 разложим трехчлены на линейные множители и выполним сокращение дроби: 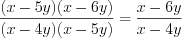 .
.Ответ: 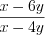 .
.
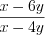 .
.Пример 4. Упростите выражение 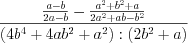 .
. 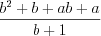 .
.
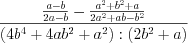 .
. 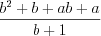 .
.Решение. Выполним последовательно действия с многочленами:
1) разложение на множители:
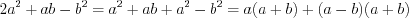
 ;
;2) вычитание многочленов по формуле 3.10
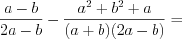

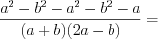
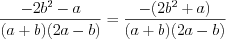 ;
;3) преобразование по формуле 3.1 и сокращение дроби
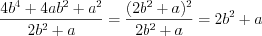 ;
;4) деление многочленов по формуле 3.12

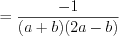 ;
;5) разложение многочлена на множители
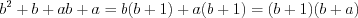 ;
;6) умножение многочленов по формуле 3.11
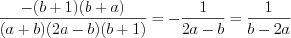 .
.Ответ: 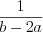 .
.
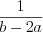 .
.Целые рациональные выражения имеют смысл при любых значениях переменных. Дробные рациональные выражения не имеют смысла при тех значениях переменных, которые обращают в нуль знаменатель дроби.
В результате некоторых преобразований может измениться область определения рационального выражения, например, в результате сокращения дроби на выражение, содержащее переменную.
Теорема Виета. Сумма корней квадратного уравнения 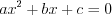 равна
равна 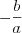 , а произведение его корней равно
, а произведение его корней равно  (при условии, что
(при условии, что 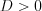 ).
).
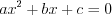 равна
равна 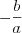 , а произведение его корней равно
, а произведение его корней равно  (при условии, что
(при условии, что 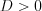 ).
).Если 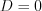 , то учитываем, что
, то учитываем, что  – двукратный корень уравнения.
– двукратный корень уравнения.
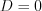 , то учитываем, что
, то учитываем, что  – двукратный корень уравнения.
– двукратный корень уравнения.Приведенным квадратным уравнением называют уравнение вида: 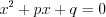 . Согласно теореме Виета, сумма корней этого уравнения равна
. Согласно теореме Виета, сумма корней этого уравнения равна 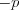 , а произведение его корней равно
, а произведение его корней равно  .
.
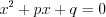 . Согласно теореме Виета, сумма корней этого уравнения равна
. Согласно теореме Виета, сумма корней этого уравнения равна 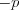 , а произведение его корней равно
, а произведение его корней равно  .
. Теорема, обратная теореме Виета. Числа  и
и  являются корнями квадратного уравнения
являются корнями квадратного уравнения 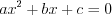
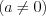 , если их сумма равна
, если их сумма равна 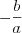 , а произведение равно
, а произведение равно  .
.
 и
и  являются корнями квадратного уравнения
являются корнями квадратного уравнения 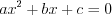
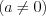 , если их сумма равна
, если их сумма равна 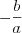 , а произведение равно
, а произведение равно  .
.
