Справочный материал
Примеры
Обратите внимание!
Видео
Модели
Пройти тесты
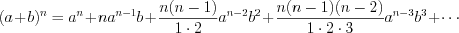
 , (3.8) где
, (3.8) где  .
.
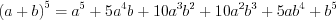
Для любых  и
и  справедливы следующие равенства:
справедливы следующие равенства:
 и
и  справедливы следующие равенства:
справедливы следующие равенства: квадрат суммы: 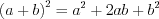 ; (3.1)
; (3.1)
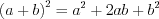 ; (3.1)
; (3.1)квадрат разности: 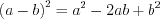 ; (3.2)
; (3.2)
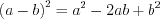 ; (3.2)
; (3.2)куб суммы: 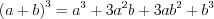 ; (3.3)
; (3.3)
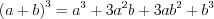 ; (3.3)
; (3.3)куб разности: 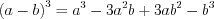 ; (3.4)
; (3.4)
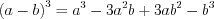 ; (3.4)
; (3.4)разность квадратов: 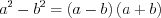 ; (3.5)
; (3.5)
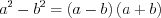 ; (3.5)
; (3.5)сумма кубов: 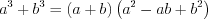 ; (3.6)
; (3.6)
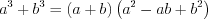 ; (3.6)
; (3.6)разность кубов: 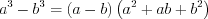 . (3.7)
. (3.7)
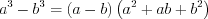 . (3.7)
. (3.7)Бином Ньютона
Биномом Ньютона называют формулу вида:
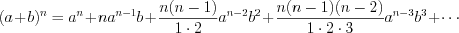
 , (3.8) где
, (3.8) где  .
.С помощью бинома Ньютона можно возвести двучлен в любую натуральную степень.
Биномиальные коэффициенты (коэффициенты при переменных) удобно вычислять, пользуясь треугольником Паскаля:

Например, используя треугольник Паскаля, запишем:
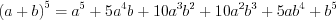
Пример 1. Упростите выражение  .
.
 .
.Пример 2. Упростите выражение 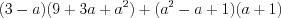 .
.
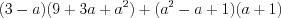 .
.Ответ: 28.
Пример 3. Найдите значение выражения 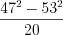 .
.
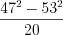 .
.Ответ: –30.
Формулы сокращенного умножения применяют при упрощении выражений, а также при вычислении значений выражений.


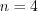 , то согласно
, то согласно 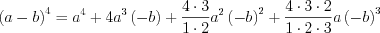
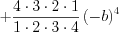
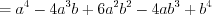
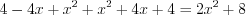
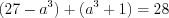
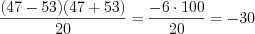 .
.